Tempco Equations
Synthesizers of 1970-era vintage were often criticized for having excessive temperature drift. In fact, proponents of digital technology advanced this as one major reason for abandoning analog technology. In addition, a number of influential authors claimed that good temperature compensation could only be achieved at a single temperature with passive compensation techniques.
It is now clear that these early ideas were incorrect. The designs used for early analog VCOs usually implemented compensation in an imprecise manner, and, additionally, only compensated some of the sources of drift. Also, it appears that the proper mathematics of compensation has not been widely appreciated. In fact, very accurate passive compensation can be attained relatively easily, even by home builders, as has been demonstrated in the VCO pages elsewhere on this site.
The present document contains the mathematical background necessary to understand passive compensation techniques for VCOs. Many of the general results may, and have been, applied to active compensation schemes also, although this topic will not be explicitly pursued here. The reader is presumed to already have a basic understanding of how exponential converters work, knowledge of elementary calculus and enough mathematical skills to fill in intermediate steps in the derivations.
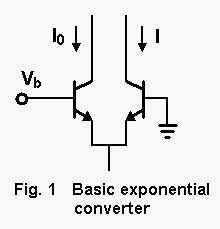 A typical standard exponential converter used in VCOs is shown in Fig. 1. It consists of a matched pair of transistors, which we will consider to be ideal. A reference current is forced through the left-hand transistor by a servo circuit (not shown). The output current is an exponential function of the differential base-emitter voltage, which in this case is just the voltage applied to the base of the left-hand transistor.
A typical standard exponential converter used in VCOs is shown in Fig. 1. It consists of a matched pair of transistors, which we will consider to be ideal. A reference current is forced through the left-hand transistor by a servo circuit (not shown). The output current is an exponential function of the differential base-emitter voltage, which in this case is just the voltage applied to the base of the left-hand transistor.
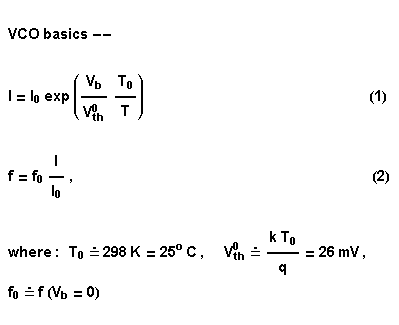 The equations for the converter's output current and the VCO's frequency are given in the first equation panel, left. Note that we write our equations in terms of the room-temperature (RT) value of the thermal voltage, in order to make the temperature dependence appear explicitly. Note also that at this point we are assuming that there are no extra sources of drift in the oscillator proper.
The equations for the converter's output current and the VCO's frequency are given in the first equation panel, left. Note that we write our equations in terms of the room-temperature (RT) value of the thermal voltage, in order to make the temperature dependence appear explicitly. Note also that at this point we are assuming that there are no extra sources of drift in the oscillator proper.
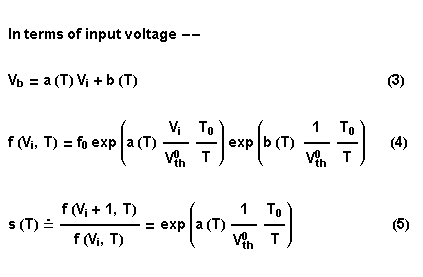 In a synthesizer VCO circuit, an input control voltage is scaled and applied to the base of the converter transistor. The scaling provides the usual 1 V / octave response and also may include temperature compensation. We will assume that the mapping from the input to the transistor base is linear, but temperature dependent, as specified in Eqn. (3). Equation (4) then gives the VCO frequency as a function of input control voltage and temperature. In understanding VCO behavior it is convenient to define a quantity called the "scale factor", defined by Eqn. (5). This is the ratio of frequencies, ideally 2, produced by a 1 V change in the input voltage. (Note that the units appear incorrect on the right side of Eqn. (5). This is because the printed "1" is actually 1 Volt. To keep track of the units more easily, we could define the voltage change by a variable, say U Volts, setting U=1 at the end of the calculation.)
In a synthesizer VCO circuit, an input control voltage is scaled and applied to the base of the converter transistor. The scaling provides the usual 1 V / octave response and also may include temperature compensation. We will assume that the mapping from the input to the transistor base is linear, but temperature dependent, as specified in Eqn. (3). Equation (4) then gives the VCO frequency as a function of input control voltage and temperature. In understanding VCO behavior it is convenient to define a quantity called the "scale factor", defined by Eqn. (5). This is the ratio of frequencies, ideally 2, produced by a 1 V change in the input voltage. (Note that the units appear incorrect on the right side of Eqn. (5). This is because the printed "1" is actually 1 Volt. To keep track of the units more easily, we could define the voltage change by a variable, say U Volts, setting U=1 at the end of the calculation.)
 With this background, we are now ready to begin calculating the converter's temperature drift. As is customary, we will define "drift" of a quantity as the fractional change in that quantity per degree of temperature change, using either the Kelvin or Celsius temperature scales. The units of drift are thus 1 / K. Often the drift value is multiplied by 100 or a million to give units of per cent / K or ppm / K. The drift is usually specified at RT. From elementary calculus, the drift may also be expressed as a logarithmic temperature derivative. This form is particularly convenient, as our temperature dependencies are often in exponential factors. Equation (6) defines what we will refer to as "absolute" drift, that is, the total drift in frequency produced by the a(T) and b(T) variables, and gives the general expression for this quantity. It is also of interest to calculate the "scale factor" drift as given by Eqn. (7).
With this background, we are now ready to begin calculating the converter's temperature drift. As is customary, we will define "drift" of a quantity as the fractional change in that quantity per degree of temperature change, using either the Kelvin or Celsius temperature scales. The units of drift are thus 1 / K. Often the drift value is multiplied by 100 or a million to give units of per cent / K or ppm / K. The drift is usually specified at RT. From elementary calculus, the drift may also be expressed as a logarithmic temperature derivative. This form is particularly convenient, as our temperature dependencies are often in exponential factors. Equation (6) defines what we will refer to as "absolute" drift, that is, the total drift in frequency produced by the a(T) and b(T) variables, and gives the general expression for this quantity. It is also of interest to calculate the "scale factor" drift as given by Eqn. (7).
A couple of additional comments about Eqns (6) and (7) are in order. Note that scale-factor drift causes a spreading out or a compressing of the musical scale and that it stems from terms that are proportional to the input voltage. It becomes zero if the factor a(T) is proportional to absolute temperature (PTAT). If the scale-factor drift is zero, then the first term in the absolute drift expression is also zero, leaving only the contribution from the b(T) term. We may refer to this latter term as representing "tuning drift", as it can be compensated by retuning the VCO.
 The next step in our derivation is to account explicitly for the nominal scaling. In other words, we assume that the converter has been adjusted for a correct Volt / octave response at RT. Thus we set the RT scale factor to 2 and obtain a specific value for the "a" coefficient at RT, as given in Eqn. 8. Substituting this result into Eqns. (4, 6, 7) yields Eqns. (9, 10, 11). These are quite general results for the temperature behavior of exponential converters and may be applied to a variety of circuit configurations. Next we will specialize these results to one specific configuration.
The next step in our derivation is to account explicitly for the nominal scaling. In other words, we assume that the converter has been adjusted for a correct Volt / octave response at RT. Thus we set the RT scale factor to 2 and obtain a specific value for the "a" coefficient at RT, as given in Eqn. 8. Substituting this result into Eqns. (4, 6, 7) yields Eqns. (9, 10, 11). These are quite general results for the temperature behavior of exponential converters and may be applied to a variety of circuit configurations. Next we will specialize these results to one specific configuration.
To see how the above equations may be applied to a real circuit we will consider the case where a temperature-compensating resistor (tempco resistor) is included in the scaling circuit so that its value multiplies the input voltage. This is usually done by putting it in the feedback path of an op amp located between the input and the transistor base. As can be seen from Eqn. (10), the a(T) and b(T) terms contribute independently to the drift, so we may temporarily set b(T) to zero and calculate its contribution later.
 Now we have that the base voltage is as given by Eqn. (12), where the constant is to be determined from the value of the tempco resistor and the requirement for proper RT scaling. We write the resistance of the tempco resistor as shown in Eqn. (13). If the constant B is zero, then the tempco resistor has a PTAT behavior and will properly compensate the scale-factor drift. If the tempco resistor does not have the ideal coefficient, then including the constant B is the correct way to describe its behavior. This is a consequence of the fundamental physics of metals, which may be studied in any good solid-state physics textbook. Equation (14) gives the relation between R(T) and a(T) and the value of the constant, which are easily obtained from Eqns. (12) and (8). Substituting these values in Eqns. (9) and (11) yields Eqns. (15) and (16) for the frequency and scale-factor drift of the VCO.
Now we have that the base voltage is as given by Eqn. (12), where the constant is to be determined from the value of the tempco resistor and the requirement for proper RT scaling. We write the resistance of the tempco resistor as shown in Eqn. (13). If the constant B is zero, then the tempco resistor has a PTAT behavior and will properly compensate the scale-factor drift. If the tempco resistor does not have the ideal coefficient, then including the constant B is the correct way to describe its behavior. This is a consequence of the fundamental physics of metals, which may be studied in any good solid-state physics textbook. Equation (14) gives the relation between R(T) and a(T) and the value of the constant, which are easily obtained from Eqns. (12) and (8). Substituting these values in Eqns. (9) and (11) yields Eqns. (15) and (16) for the frequency and scale-factor drift of the VCO.
At this point, we introduce the temperature coefficient alpha of the tempco resistor. This is defined and evaluated in Eqn. (17). If the error term B is zero then the tempco is the reciprocal of room temperature, or the familiar value of 3350 ppm / K. The next equation, Eqn. (18) is our main result. It shows how the constant B may be calculated from measured quantities, either the residual scale-factor drift or the tempco coefficient. Given this value of B, a compensating voltage may be added to the transistor base to achieve correct scale-factor compensation. The value of this voltage is given by Eqn. (19).
 Finally, we consider the contribution of the b(T) tuning-drift term. If high-quality modern circuit components are used for the converter, then the intrinsic value of b(T) will be very small. The importance of this contribution is that we may deliberately add an offset voltage b to the transistor base to deliberately produce a "counter drift" to cancel other sources of tuning drift, such as the drift caused by the temperature coefficient of the integrating capacitor in the oscillator core circuitry. For this reason, we will assume that b is deliberately added and independent of temperature. Since we have already calculated the scale-factor drift, we may assume an ideal tempco resistor. The result for the counter drift is then given by Eqn. (21), which states that every 1 mV of deliberately added offset will cancel -129 ppm / K of residual tuning drift.
Finally, we consider the contribution of the b(T) tuning-drift term. If high-quality modern circuit components are used for the converter, then the intrinsic value of b(T) will be very small. The importance of this contribution is that we may deliberately add an offset voltage b to the transistor base to deliberately produce a "counter drift" to cancel other sources of tuning drift, such as the drift caused by the temperature coefficient of the integrating capacitor in the oscillator core circuitry. For this reason, we will assume that b is deliberately added and independent of temperature. Since we have already calculated the scale-factor drift, we may assume an ideal tempco resistor. The result for the counter drift is then given by Eqn. (21), which states that every 1 mV of deliberately added offset will cancel -129 ppm / K of residual tuning drift.
To summarize, we have seen how to design an accurately compensated exponential converter by correcting for the non-ideality of the tempco resistor employed and by compensating for op amp offsets and other sources of drift by deliberately adding an offset voltage to the converter.
Back Home
 A typical standard exponential converter used in VCOs is shown in Fig. 1. It consists of a matched pair of transistors, which we will consider to be ideal. A reference current is forced through the left-hand transistor by a servo circuit (not shown). The output current is an exponential function of the differential base-emitter voltage, which in this case is just the voltage applied to the base of the left-hand transistor.
A typical standard exponential converter used in VCOs is shown in Fig. 1. It consists of a matched pair of transistors, which we will consider to be ideal. A reference current is forced through the left-hand transistor by a servo circuit (not shown). The output current is an exponential function of the differential base-emitter voltage, which in this case is just the voltage applied to the base of the left-hand transistor.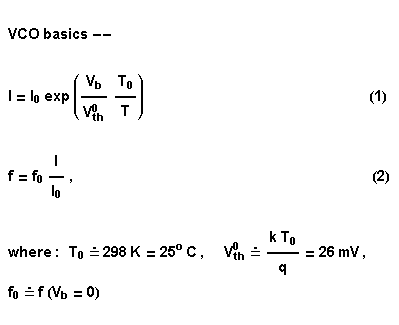 The equations for the converter's output current and the VCO's frequency are given in the first equation panel, left. Note that we write our equations in terms of the room-temperature (RT) value of the thermal voltage, in order to make the temperature dependence appear explicitly. Note also that at this point we are assuming that there are no extra sources of drift in the oscillator proper.
The equations for the converter's output current and the VCO's frequency are given in the first equation panel, left. Note that we write our equations in terms of the room-temperature (RT) value of the thermal voltage, in order to make the temperature dependence appear explicitly. Note also that at this point we are assuming that there are no extra sources of drift in the oscillator proper.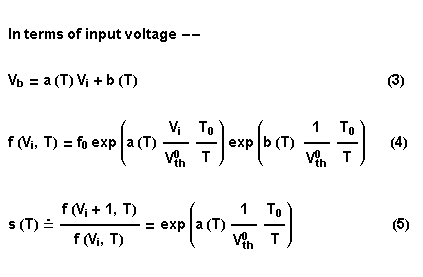 In a synthesizer VCO circuit, an input control voltage is scaled and applied to the base of the converter transistor. The scaling provides the usual 1 V / octave response and also may include temperature compensation. We will assume that the mapping from the input to the transistor base is linear, but temperature dependent, as specified in Eqn. (3). Equation (4) then gives the VCO frequency as a function of input control voltage and temperature. In understanding VCO behavior it is convenient to define a quantity called the "scale factor", defined by Eqn. (5). This is the ratio of frequencies, ideally 2, produced by a 1 V change in the input voltage. (Note that the units appear incorrect on the right side of Eqn. (5). This is because the printed "1" is actually 1 Volt. To keep track of the units more easily, we could define the voltage change by a variable, say U Volts, setting U=1 at the end of the calculation.)
In a synthesizer VCO circuit, an input control voltage is scaled and applied to the base of the converter transistor. The scaling provides the usual 1 V / octave response and also may include temperature compensation. We will assume that the mapping from the input to the transistor base is linear, but temperature dependent, as specified in Eqn. (3). Equation (4) then gives the VCO frequency as a function of input control voltage and temperature. In understanding VCO behavior it is convenient to define a quantity called the "scale factor", defined by Eqn. (5). This is the ratio of frequencies, ideally 2, produced by a 1 V change in the input voltage. (Note that the units appear incorrect on the right side of Eqn. (5). This is because the printed "1" is actually 1 Volt. To keep track of the units more easily, we could define the voltage change by a variable, say U Volts, setting U=1 at the end of the calculation.) With this background, we are now ready to begin calculating the converter's temperature drift. As is customary, we will define "drift" of a quantity as the fractional change in that quantity per degree of temperature change, using either the Kelvin or Celsius temperature scales. The units of drift are thus 1 / K. Often the drift value is multiplied by 100 or a million to give units of per cent / K or ppm / K. The drift is usually specified at RT. From elementary calculus, the drift may also be expressed as a logarithmic temperature derivative. This form is particularly convenient, as our temperature dependencies are often in exponential factors. Equation (6) defines what we will refer to as "absolute" drift, that is, the total drift in frequency produced by the a(T) and b(T) variables, and gives the general expression for this quantity. It is also of interest to calculate the "scale factor" drift as given by Eqn. (7).
With this background, we are now ready to begin calculating the converter's temperature drift. As is customary, we will define "drift" of a quantity as the fractional change in that quantity per degree of temperature change, using either the Kelvin or Celsius temperature scales. The units of drift are thus 1 / K. Often the drift value is multiplied by 100 or a million to give units of per cent / K or ppm / K. The drift is usually specified at RT. From elementary calculus, the drift may also be expressed as a logarithmic temperature derivative. This form is particularly convenient, as our temperature dependencies are often in exponential factors. Equation (6) defines what we will refer to as "absolute" drift, that is, the total drift in frequency produced by the a(T) and b(T) variables, and gives the general expression for this quantity. It is also of interest to calculate the "scale factor" drift as given by Eqn. (7). The next step in our derivation is to account explicitly for the nominal scaling. In other words, we assume that the converter has been adjusted for a correct Volt / octave response at RT. Thus we set the RT scale factor to 2 and obtain a specific value for the "a" coefficient at RT, as given in Eqn. 8. Substituting this result into Eqns. (4, 6, 7) yields Eqns. (9, 10, 11). These are quite general results for the temperature behavior of exponential converters and may be applied to a variety of circuit configurations. Next we will specialize these results to one specific configuration.
The next step in our derivation is to account explicitly for the nominal scaling. In other words, we assume that the converter has been adjusted for a correct Volt / octave response at RT. Thus we set the RT scale factor to 2 and obtain a specific value for the "a" coefficient at RT, as given in Eqn. 8. Substituting this result into Eqns. (4, 6, 7) yields Eqns. (9, 10, 11). These are quite general results for the temperature behavior of exponential converters and may be applied to a variety of circuit configurations. Next we will specialize these results to one specific configuration. Now we have that the base voltage is as given by Eqn. (12), where the constant is to be determined from the value of the tempco resistor and the requirement for proper RT scaling. We write the resistance of the tempco resistor as shown in Eqn. (13). If the constant B is zero, then the tempco resistor has a PTAT behavior and will properly compensate the scale-factor drift. If the tempco resistor does not have the ideal coefficient, then including the constant B is the correct way to describe its behavior. This is a consequence of the fundamental physics of metals, which may be studied in any good solid-state physics textbook. Equation (14) gives the relation between R(T) and a(T) and the value of the constant, which are easily obtained from Eqns. (12) and (8). Substituting these values in Eqns. (9) and (11) yields Eqns. (15) and (16) for the frequency and scale-factor drift of the VCO.
Now we have that the base voltage is as given by Eqn. (12), where the constant is to be determined from the value of the tempco resistor and the requirement for proper RT scaling. We write the resistance of the tempco resistor as shown in Eqn. (13). If the constant B is zero, then the tempco resistor has a PTAT behavior and will properly compensate the scale-factor drift. If the tempco resistor does not have the ideal coefficient, then including the constant B is the correct way to describe its behavior. This is a consequence of the fundamental physics of metals, which may be studied in any good solid-state physics textbook. Equation (14) gives the relation between R(T) and a(T) and the value of the constant, which are easily obtained from Eqns. (12) and (8). Substituting these values in Eqns. (9) and (11) yields Eqns. (15) and (16) for the frequency and scale-factor drift of the VCO. Finally, we consider the contribution of the b(T) tuning-drift term. If high-quality modern circuit components are used for the converter, then the intrinsic value of b(T) will be very small. The importance of this contribution is that we may deliberately add an offset voltage b to the transistor base to deliberately produce a "counter drift" to cancel other sources of tuning drift, such as the drift caused by the temperature coefficient of the integrating capacitor in the oscillator core circuitry. For this reason, we will assume that b is deliberately added and independent of temperature. Since we have already calculated the scale-factor drift, we may assume an ideal tempco resistor. The result for the counter drift is then given by Eqn. (21), which states that every 1 mV of deliberately added offset will cancel -129 ppm / K of residual tuning drift.
Finally, we consider the contribution of the b(T) tuning-drift term. If high-quality modern circuit components are used for the converter, then the intrinsic value of b(T) will be very small. The importance of this contribution is that we may deliberately add an offset voltage b to the transistor base to deliberately produce a "counter drift" to cancel other sources of tuning drift, such as the drift caused by the temperature coefficient of the integrating capacitor in the oscillator core circuitry. For this reason, we will assume that b is deliberately added and independent of temperature. Since we have already calculated the scale-factor drift, we may assume an ideal tempco resistor. The result for the counter drift is then given by Eqn. (21), which states that every 1 mV of deliberately added offset will cancel -129 ppm / K of residual tuning drift.